A. Pengertian Momentum.Momentum suatu benda adalah hasil kali massa dan kecepatan.
Dirumuskan dengan persamaan:
p = m.v m = massa ( kg)
v = kecepatan ( m/s )
p = momentum ( kg.m/s )
Momentum juga disebut jumlah gerak.
Momentum adalah besaran vector. Momentum 45 kgm/s ke utara berbeda dengan momentum 45 kgm/s ke selatan, walaupun nilai keduanya sama. Penjumlahan momentum mengikuti aturan penjumlahan vector. Misal momentum p1 dan p2 membentuk sudut α , maka resultan/ jumlah kedua momentum tersebut dapayt dituliskan dengan persamaan :
p1
p
p2
α –––––––––––––––––––––––––––––––
p = √ p12 + p22 + 2 p1 p2 cos α
B. Pengetian Impuls.Impuls adalah hasil kali antara gaya yang bekerja dan selang waktu gaya itu bekerja. Impuls juga sering disebut pukulan.
Dirumuskan dengan persamaan :
I = F. ∆t F = gaya ( N )
∆t = selang waktu ( s )
I = Impuls ( Ns )
Impuls merupakan besaran vector.
C. Hubungan antara imupls dan momentum.
Sebuah benda massa m mula-mula bergerak dengan kecepatan v1, kemudian dipukul dengan gaya F hingga kecepatannya menjadi v2, seperti gambar di bawah, maka besarnya impuls yang bekerja pada benda tersebut adalah:
∆t
v1
v2
F
m m
Sesuai dengan hukum II Newton:
I = F. ∆t , karena
v2 – v1
F = m.a dan a = –––––––––––, maka :
∆t
v2 – v1
I = m.–––––– . ∆t
∆t
I = m (v2 – v1 ) –––––> I = m v2 – m v1 atau I = p2 – p1
Dapat juga dituls I = ∆p ( Impuls merupakan perubahan momentum benda )
Contoh Soal
Sebuah benda massa 5 kg bergerak dengan kecepatan 10m/s. Hitunglah momentum yang dimiliki benda!
Penyelesian : Diketahui : m = 5 kg; v = 10 m/s
Ditanya : p = …?
Jaab : p = m.v = 5.10 = 50 kgm/s
Sebuah benda mula-mula bergerak ke utara dengan kecepatan 6 m/s, kemudian berbelok ke barat dengan kecepatan 8 m/s. Apabila massa benda 50 kg, berpakah momentum total yang dimiliki benda ?
Penyelesaian : Diketahui : v1 = 6 m/s; v2 = 8 m/s; m = 5 kg
Ditanya : p = …?
Jawab : p1 = m. v1 = 50.6 = 300 kgm/s
p1
p
P2 P2 = m. v2 = 50.8 = 400 kgm/s
––––––– –––––––––
p = √ p12 + p22 = √ 3002 + 4002 = 500 kgm/s
Sebuah gaya 25 N bekerja pada sebuah benda dalam selang waktu 0,2 sekon. Hitunglah impuls yang dikerjakan gaya tersebut pada benda
Penyelesaian : Diketahui : F = 25 N; ∆t = 0,2 s
Ditanya : I = …?
Jawab : I = F. ∆t = 25. 0,2 = 5 Ns
Sebuah bola massanya 50 gram dilempar dengan kecepatan 10 m/s, kemudian dipukul dengan gaya F hingga kecepatannya 20 m/s berlawanan arah dengan kecepatan semula.
Hitunglah impuls yang dikerjakan oleh gaya tersebut!
Jika besarnya gaya F = 150 N, berapa lama pemukul menyentuh bola?
Penyelesaian : Diketahui : m = 50 gram = 50.10–3 kg; v1 = – 10 m/s;
v2 = 20 m/s
Ditanya : a. I = …?
b. Jika F = 150 N –––> ∆t = …?
Jawab : a. I = m.( v2 – v1 ) = 50.10–3 [20 – (-10)]
= 50.10–3. 30 = 1500.10–3 = 1,5 Ns
b. I = F. ∆t ––––> 1,5 = 150. ∆t –––> ∆t = 0,01 s
D. Hukum Kekekalan Momentum dan Tumbukan.
“Jumlah momentum suatu sistem sebelum dan sesudah tumbukan akan selalu tetap”
Pernyataan di atas disebut hukum kekekalan momentum dan ditulis dengan persamaan:
m1.v1 + m2.v2 = m1.v1’ + m2.v2’ m1 = massa benda 1
m2 = massa benda 2
v1 = kecepatan benda 1 sebelum tumbukan
v2 = kecepatan benda 2 sebelum tumbukan
v1’ = kecepatan benda 1 sesudah tumbukan
v2’ = kecepatan benda 2 sesudah tumbukan
Jenis-jenis Tumbukan
a. Tumbukan lenting sempurna (elastis sempurna)
Tumbukan lenting sempurna yaitu tumbukan dimana tidak ada energi kinetik yang hilang dari sistem. Dalam tumbukan ini berlaku hukum kekekalan momentum dan hukum kekekalan energi kinetik.
Dalam hal ini berlaku persamaan :
m1.v1 + m2.v2 = m1.v1’ + m2.v2’ ……………………….(1) dan
½ m1.v12 + ½ m2.v22 = ½ m1.(v1’)2 + ½ m2.(v2’)2 ……..(2)
Dengan membagi persamaan (2) dengan persamaan (1), maka akan didapatkan
persamaan : v1 + v1’ = v2 + v2’
b. Tumbukan tidak lenting sama sekali
Pada tumbukan tidak lenting sama sekali, sesudah tumbukan kedua benda bergabung menjadi satu dan bergerak bersama-sama. Dengan demikian, maka kecepatan kedua benda setelah bertumbukan adalah sama.: v1’ = v2’ = v’
Pada tumbukan ini persamaan hukum kekekalan momentum dapat ditulis sbb:
m1.v1 + m2.v2 = m1.v1’ + m2.v2’, karena v1’ = v2’ = v’, maka
m1.v1 + m2.v2 = m1.v’ + m2.v’
atau dapat juga ditulis :
m1.v1 + m2.v2 = (m1 + m2).v’
v’ = kecepatan benda setelah tumbukan ( m/s )
Contoh Soal
1. Seorang penembak memegang sebuah senapan 3 kg dengan bebas sehingga membiarkan senapan bergerak secara bebas ketika menembakkan sebutir peluru bermassa 5 gram. Peluru itu keluar dari moncong senapan dengan kecepatan horisontal 300 m/s. Berapa kecepatan hentakan senapan ketika peluru ditembakkan?
Penyelesaian :
Diketahui : Benda 1 (senapan) m1 = 3 kg; v1 = 0
Benda 2 (peluru ) m2 = 5 g ; v2 = 0 ; v2’ = 300 m/s.
Ditanya : v1’ = …?
Jawab :Gunakanlah hukum kekekalan momentum!
m1.v1 + m2.v2 = m1.v1’ + m2.v2’
3.0 + 5.10–3.0 = 3. v1’ + 5.10–3. 300
0 = 3. v1’ + 1,5
–3. v1’ = 1,5 –––––––––> v1’ = 1,5/–3 = –0,5 m/s
2. Dua nelayan sedang berada di perahu yang bergerak dengan kecepatan 2 m/s. Massa perahu 200 kg dan massa tiap nelayan 50 kg. Berapa kecepatan perah sesaat sesudah :
a. Seorang nelayan terjatuh
b. Seorang nelayan melompat dari perahu dengan kecepatan 4 m/s searah dengan gerak perahu
c. Seorang nelayan melompat dari perahu dengan kecepatan 4 m/s berlawanan arah dengan gerak perahu
Penyelesaian :
Diketahui : m1 = massa perahu + massa satu orang
= 200 + 50 = 250 kg
m2 = massa satu orang = 50 kg
v1 = v2 = v = 2 m/s;
Ditanya : a. v1’ = …? Jika v2’ = 0
b. v1’ = …? Jika v2’ = 4 m/s
c. v1’ = …? Jika v2’ = – 4 m/s
Jawab : Gunakanlah hokum kekekalan momentum
a. m1.v1 + m2.v2 = m1.v1’ + m2.v2’
250.2 + 50.2 = 250. v1’ + 50. 0
500 + 100 = 250. v1’ + 0
250. v1’ = 600 –––––––––> v1’ = 600/250 = 2,4 m/s
b. m1.v1 + m2.v2 = m1.v1’ + m2.v2’
250.2 + 50.2 = 250. v1’ + 50. 4
500 + 100 = 250. v1’ + 200
250. v1’ = 400 –––––––––> v1’ = 400/250 = 1,6 m/s
c. m1.v1 + m2.v2 = m1.v1’ + m2.v2’
250.2 + 50.2 = 250. v1’ + 50.(– 4)
500 + 100 = 250. v1’ – 200
250. v1’ = 800 –––––––––> v1’ = 800/250 = 3,2 m/s
3. Sebuah bola dengan massa 40 gram bergerak ke kanan dengan kelajuan 30 m/s menumbuk bola lain yang massanya 80 gram yang mula-mulla diam. Jika tumbukan lenting sempurna, berapakah kecepatan masing-masing bola setelah tumbukan?
Penyelesaian :
Diketahui : m1 = 40 gram; m2 = 80 gram;
v1 = 30 m/s; v2 = 0
Ditanya : v1’ = …? dan v2’ = …? (tumbukan lenting sempurna)
Jawab : Gunakanlah persamaan : v1 + v1’ = v2 + v2’
30 + v1’ = 0 + v2’ –––> v2’ = 30 + v1’
Hukum kekekalan momentum:
m1.v1 + m2.v2 = m1.v1’ + m2.v2’
40.30 + 80.0 = 40. v1’ + 80.( 30 + v1’)
1200 + 0 = 40. v1’ + 2400 + 80.v1’
1200 – 2400 = 120. v1’
–1200 = 120. v1’ ––––––> v1’ = –1200/120 = –10 m/s
Dari hasil v1’ = –10 m/s, maka v2’ = 30 + (–10) ––––> v2’ = 20 m/s
Tanda (–) menandakan bahwa arah kecepatan berlawanan arah dengan arah semula
4. Dua buah bola masing-masing massanya 2 kg dan 4 kg bergerak saling mendekati dengan kecepatan masing-masing 4 m/s dan 0,5 m/s, hingga saling bertumbukan. JIka tunbukan tidak lenting sama sekali, hitunglah kecepatan kedua bola setelah bertumbukan!
Penyelesaian :
Diketahui : m1 = 2 kg; m2 = 4 kg;
v1 = 4 m/s; v2 = –0,5 m/s
Ditanya : v1’ = …? dan v2’ = …? (tumbukan tidak lenting sama sekali)
Jawab : Gunakanlah persamaan : v1’ = v2’ = v’
Hukum kekekalan momentum:
m1.v1 + m2.v2 = m1.v1’ + m2.v2’
2. 4 + 4.(–0,5) = 2. v’ + 4.v’
8 – 2 = 6. v’ ––––––> 6. v’ = 6 ––––> v’ =6/6 = 1 m/s
Jadi kecepatan kedua benda setelah tumbukan adalah 1 m/s.
Soal Latihan:
Hitung besarnya momentum sebuak truk yang massanya 2 ton yang bergerak dengan kecepatan 20 m/s.
Sebuah benda bergeak dengan kecepatan 72 km/jam. Momentum yang dimiliki benda tersebut adalah 2.105 kgm/s. Hitunglah massa benda!
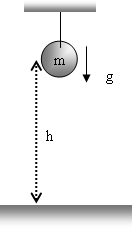
ebuah bneda massa 4kg dijatuhkan tanpa kecepatan awal dari ketinggian 45 m. Berapa momentum bneda saat menumbuk tanah?
Sebuah benda massa 3 kg diberi gaya kontan 12 N sehingga kecepatannya betambah dari 10 m/s menjadi 18 m/s. Hitunglah :
Impuls yang bekerja pada benda
Lama gaya itu bereaksi/ bekerja
Sebuah benda massa 4 kg bergerak dengan kecepatan 20 m/s dihentikan oleh suatu gaya konstan 50 N dalam selang waktu ∆t. Hiutnglah :
Impuls gaya
Selang waktu gaya bekerja (∆t.)
Sebuah peluru bermassa 20 gram ditembakkan horizontal dengan kecepatan 250 m/s. Berapa kecepatan senapan endorong bahu penembak?
Sebuah bus massa 10 ton bergerak dengan kelajuan 4 m/s, menabrak sebuah truk massa 20 ton yang seang bergerak dengan arah berlawanan dan sesudah bertabrakan keduanya berhenti. Berapa kelajuan truk itu sesaat sebelum bertabrakan?
Sebuah balok massa 2 kg meluncur dengan kecepatan 10 m/s spanjang lantai licin danmenumbuk balok lain yang mula-mula diam. Jika tumbukan lenting sempurna, hitunglah kecepatan masing-masing balok setelah tumbukan!
Sebuah kereta dinamik massa 2 kg begerak ke kanan dengan kecepatan 4 m/s menumbuk lenting sempurna kereta dinamik lain massa 4 kg yang sedang bergerak ke kiri dengan kecepatan 1 m/s. Hitung kecepatan masing-masing keret sesudah bertumbukan!
Dua benda massanya sama yaitu 2 kg, bergerak berlawanan arah dengan kecepatan masing-masing 10 m/s dan 5 m/s. Sesudah tumbukan kedua benda menyatu. Tentukan :
Kecepatan kedua benda sesudah tumbukan.
Energy kinetic yang hilang selama proses tumbukan.
ENIS-JENIS TUMBUKAN
Perlu anda ketahui bahwa biasanya dua benda yang bertumbukan bergerak mendekat satu dengan yang lain dan setelah bertumbukan keduanya bergerak saling menjauhi. Ketika benda bergerak, maka tentu saja benda memiliki kecepatan. Karena benda tersebut mempunyai kecepatan (dan massa), maka benda itu pasti memiliki momentum (p = mv) dan juga Energi Kinetik (EK = ½ mv2).
Nah, pada kesempatan ini kita akan mempelajari jenis-jenis tumbukan antara dua benda dan mencoba melihat hubungannya dengan Kekekalan Momentum dan Kekekalan Energi Kinetik. Napa yang ditinjau kekekalan momentum dan kekekalan energi kinetik-nya ? bukannya Cuma momentum dan energi kinetik ? yupz… maksudnya begini, ketika benda bergerak saling mendekati sebelum tumbukan, kedua benda itu memiliki Momentum dan Energi Kinetik. Yang menjadi persoalan, bagaimana dengan Momentum dan Energi Kinetik kedua benda tersebut setelah bertumbukan ? apakah momentum dan energi kinetik kedua benda ketika sebelum tumbukan = momentum dan energi kinetik benda setelah tumbukan ? agar dirimu semakin memahaminya, mari kita bahas jenis-jenis tumbukan satu persatu dan meninjau kekekalan momentum dan kekekalan energi kinetik pada kedua benda yang bertumbukan.
Secara umum terdapat beberapa jenis tumbukan, antara lain Tumbukan lenting sempurna, Tumbukan lenting sebagian dan Tumbukan tidak lenting sama sekali.
TUMBUKAN LENTING SEMPURNA
Tumbukan lenting sempurna tu maksudnya bagaimanakah ? Dua benda dikatakan melakukan Tumbukan lenting sempurna jika Momentum dan Energi Kinetik kedua benda sebelum tumbukan = momentum dan energi kinetik setelah tumbukan. Dengan kata lain, pada tumbukan lenting sempurna berlaku Hukum Kekekalan Momentum dan Hukum Kekekalan Energi Kinetik.
Hukum Kekekalan Momentum dan Hukum Kekekalan Energi Kinetik berlaku pada peristiwa tumbukan lenting sempurna karena total massa dan kecepatan kedua benda sama, baik sebelum maupun setelah tumbukan. Hukum Kekekalan Energi Kinetik berlaku pada Tumbukan lenting sempurna karena selama tumbukan tidak ada energi yang hilang. Untuk memahami konsep ini, coba jawab pertanyaan gurumuda berikut ini. Ketika dua bola billiard atau dua kelereng bertumbukan, apakah anda mendengar bunyi yang diakibatkan oleh tumbukan itu ? atau ketika mobil atau sepeda motor bertabrakan, apakah ada bunyi yang dihasilkan ? pasti ada bunyi dan juga panas yang muncul akibat benturan antara dua benda. Bunyi dan panas ini termasuk energi. Jadi ketika dua benda bertumbukan dan menghasilkan bunyi dan panas, maka ada energi yang hilang selama proses tumbukan tersebut. Sebagian Energi Kinetik berubah menjadi energi panas dan energi bunyi. Dengan kata lain, total energi kinetik sebelum tumbukan tidak sama dengan total energi kinetik setelah tumbukan.
Nah, benda-benda yang mengalami Tumbukan Lenting Sempurna tidak menghasilkan bunyi, panas atau bentuk energi lain ketika terjadi tumbukan. Tidak ada Energi Kinetik yang hilang selama proses tumbukan. Dengan demikian, kita bisa mengatakan bahwa pada peritiwa Tumbukan Lenting Sempurna berlaku Hukum Kekekalan Energi Kinetik.
Apakah tumbukan lenting sempurna dapat kita temui dalam kehidupan sehari-hari ? Tidak…. Tumbukan lenting sempurna merupakan sesuatu yang sulit kita temukan dalam kehidupan sehari-hari. Paling tidak ada ada sedikit energi panas dan bunyi yang dihasilkan ketika terjadi tumbukan. Salah satu contoh tumbukan yang mendekati lenting sempurna adalah tumbukan antara dua bola elastis, seperti bola billiard. Untuk kasus tumbukan bola billiard, memang energi kinetik tidak kekal tapi energi total selalu kekal. Lalu apa contoh Tumbukan lenting sempurna ? contoh jenis tumbukan ini tidak bisa kita lihat dengan mata telanjang karena terjadi pada tingkat atom, yakni tumbukan antara atom-atom dan molekul-molekul. Istirahat dulu ah…
Sekarang mari kita tinjau persamaan Hukum Kekekalan Momentum dan Hukum Kekekalan Energi Kinetik pada perisitiwa Tumbukan Lenting Sempurna. Untuk memudahkan pemahaman dirimu, perhatikan gambar di bawah.
Dua benda, benda 1 dan benda 2 bergerak saling mendekat. Benda 1 bergerak dengan kecepatan v1 dan benda 2 bergerak dengan kecepatan v2. Kedua benda itu bertumbukan dan terpantul dalam arah yang berlawanan. Perhatikan bahwa kecepatan merupakan besaran vektor sehingga dipengaruhi juga oleh arah. Sesuai dengan kesepakatan, arah ke kanan bertanda positif dan arah ke kiri bertanda negatif. Karena memiliki massa dan kecepatan, maka kedua benda memiliki momentum (p = mv) dan energi kinetik (EK = ½ mv2). Total Momentum dan Energi Kinetik kedua benda sama, baik sebelum tumbukan maupun setelah tumbukan.
Secara matematis, Hukum Kekekalan Momentum dirumuskan sebagai berikut :
Keterangan :
m1 = massa benda 1, m2 = massa benda 2
v1 = kecepatan benda sebelum tumbukan dan v2 = kecepatan benda 2 Sebelum tumbukan
v’1 = kecepatan benda Setelah tumbukan, v’2 = kecepatan benda 2 setelah tumbukan
Jika dinyatakan dalam momentum,
m1v1 = momentum benda 1 sebelum tumbukan, m1v’1 = momentum benda 1 setelah tumbukan
m2v2 = momentum benda 2 sebelum tumbukan, m2v’2 = momentum benda 2 setelah tumbukan
Pada Tumbukan Lenting Sempurna berlaku juga Hukum Kekekalan Energi Kinetik. Secara matematis dirumuskan sebagai berikut :
Kita telah menurunkan 2 persamaan untuk Tumbukan Lenting Sempurna, yakni persamaan Hukum Kekekalan Momentum dan Persamaan Hukum Kekekalan Energi Kinetik. Ada suatu hal yang menarik, bahwa apabila hanya diketahui massa dan kecepatan awal, maka kecepatan setelah tumbukan bisa kita tentukan menggunakan suatu persamaan lain. Persamaan ini diturunkan dari dua persamaan di atas. Persamaan apakah itu ? nah, mari kita turunkan persamaan tersebut… dipahami perlahan-lahan ya
Sekarang kita tulis kembali persamaan Hukum Kekekalan Momentum :
Kita tulis kembali persamaan Hukum Kekekalan Energi Kinetik :
Kita tulis kembali persamaan ini menjadi :
Ini merupakan salah satu persamaan penting dalam Tumbukan Lenting sempurna, selain persamaan Kekekalan Momentum dan persamaan Kekekalan Energi Kinetik. Persamaan 3 menyatakan bahwa pada Tumbukan Lenting Sempurna, laju kedua benda sebelum dan setelah tumbukan sama besar tetapi berlawanan arah, berapapun massa benda tersebut.
Koofisien elastisitas Tumbukan Lenting Sempurna
Wah, istilah baru lagi ne… apaan sie koofisien elastisitas ? sebelum gurumuda menjelaskan apa itu koofisien elastisitas, mari kita obok2 lagi rumus fisika. Kali ini giliran persamaan 3…
Kita tulis lagi persamaan 3 :
Perbandingan negatif antara selisih kecepatan benda setelah tumbukan dengan selisih kecepatan benda sebelum tumbukan disebut sebagai koofisien elatisitas alias faktor kepegasan (dalam buku Karangan Bapak Marthen Kanginan disebut koofisien restitusi). Untuk Tumbukan Lenting Sempurna, besar koofisien elastisitas = 1. ini menunjukkan bahwa total kecepatan benda setelah tumbukan = total kecepatan benda sebelum tumbukan. Lambang koofisien elastisitas adalah e. Secara umum, nilai koofisien elastisitas dinyatakan dengan persamaan :
e = koofisien elastisitas = koofisien restitusi, faktor kepegasan, angka kekenyalan, faktor keelastisitasan
TUMBUKAN LENTING SEBAGIAN
Pada pembahasan sebelumnya, kita telah belajar bahwa pada Tumbukan Lenting Sempurna berlaku Hukum Kekekalan Momentum dan Hukum Kekekakalan Energi Kinetik. Nah, bagaimana dengan tumbukan lenting sebagian ?
Pada tumbukan lenting sebagian, Hukum Kekekalan Energi Kinetik tidak berlaku karena ada perubahan energi kinetik terjadi ketika pada saat tumbukan. Perubahan energi kinetik bisa berarti terjadi pengurangan Energi Kinetik atau penambahan energi kinetik. Pengurangan energi kinetik terjadi ketika sebagian energi kinetik awal diubah menjadi energi lain, seperti energi panas, energi bunyi dan energi potensial. Hal ini yang membuat total energi kinetik akhir lebih kecil dari total energi kinetik awal. Kebanyakan tumbukan yang kita temui dalam kehidupan sehari-hari termasuk dalam jenis ini, di mana total energi kinetik akhir lebih kecil dari total energi kinetik awal. Tumbukan antara kelereng, tabrakan antara dua kendaraan, bola yang dipantulkan ke lantai dan lenting ke udara, dll.
Sebaliknya, energi kinetik akhir total juga bisa bertambah setelah terjadi tumbukan. Hal ini terjadi ketika energi potensial (misalnya energi kimia atau nuklir) dilepaskan. Contoh untuk kasus ini adalah peristiwa ledakan.
Suatu tumbukan lenting sebagian biasanya memiliki koofisien elastisitas (e) berkisar antara 0 sampai 1. Secara matematis dapat ditulis sebagai berikut :
Bagaimana dengan Hukum Kekekalan Momentum ? Hukum Kekekalan Momentum tetap berlaku pada peristiwa tumbukan lenting sebagian, dengan anggapan bahwa tidak ada gaya luar yang bekerja pada benda-benda yang bertumbukan.







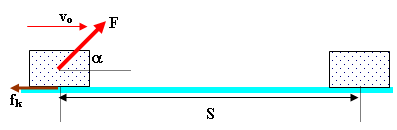
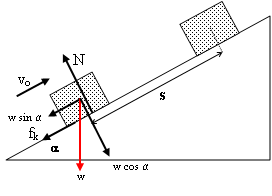
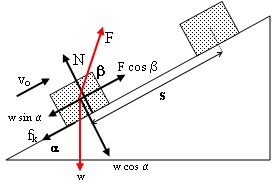
 atau
atau 


 atau
atau 
























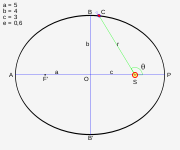

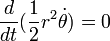
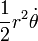 adalah "areal velocity".
adalah "areal velocity".